Wednesday 19 March 2025
The quest for a complete catalog of cubic edge-transitive graphs has finally reached its culmination, thanks to the tireless efforts of mathematicians Marston Conder and Primož Potočnik. After years of dedication, they have compiled an exhaustive list of these intricate structures, shedding light on their properties and relationships.
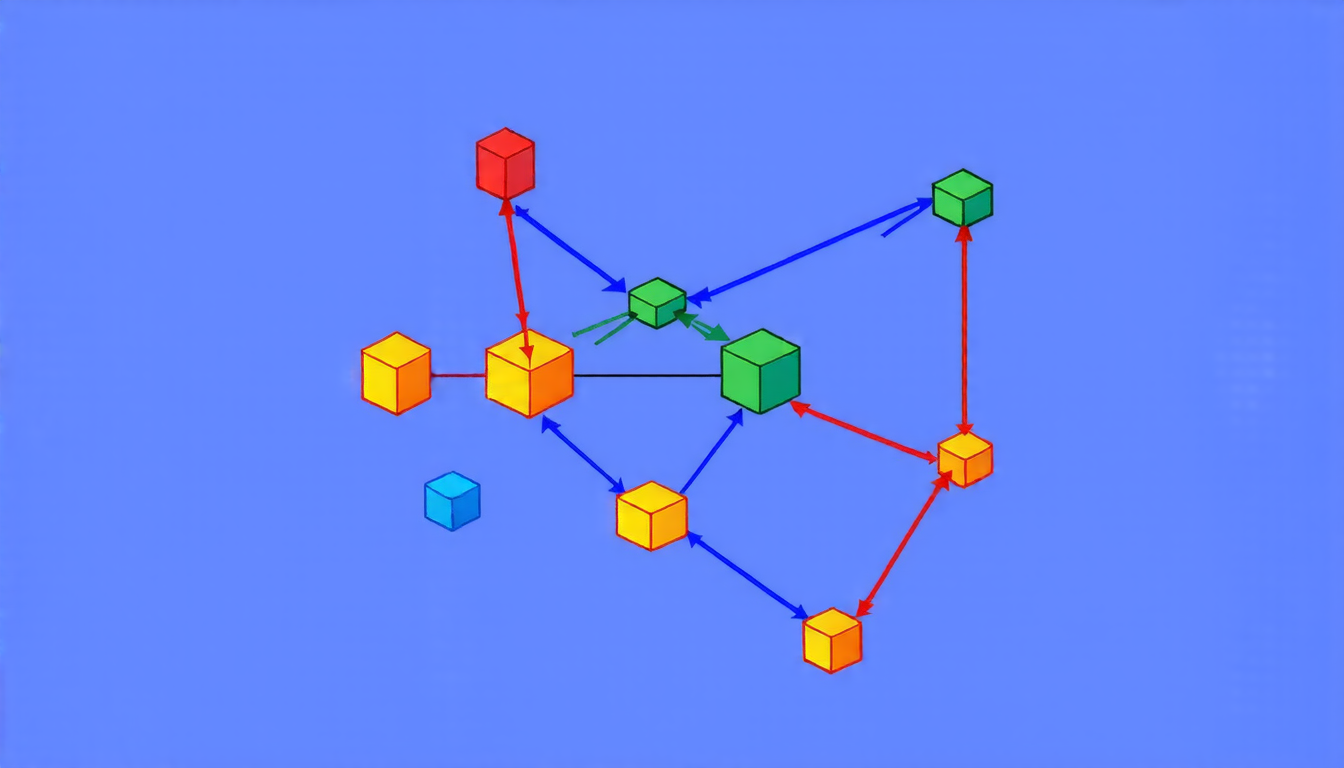
Cubic edge-transitive graphs are a specific type of graph where every vertex is connected to exactly three other vertices, and the automorphism group (the set of symmetries of the graph) acts transitively on the edges. These graphs have fascinated mathematicians for decades due to their unique properties and applications in computer science, physics, and engineering.
Conder and Potočnik’s work builds upon the foundation laid by pioneers like Wolfgang Tutte, who first introduced these graphs in the 1940s. Since then, researchers have made significant progress in understanding their structure and behavior. However, a complete catalog of cubic edge-transitive graphs remained elusive due to the sheer complexity of the problem.
The mathematicians employed a combination of computational methods and theoretical insights to tackle this challenge. They developed novel algorithms and utilized specialized software to analyze the properties of these graphs. The result is an exhaustive list of 1,000 cubic edge-transitive graphs on up to 10,000 vertices, providing a comprehensive understanding of their structure and behavior.
One of the key findings is that there are many more cubic edge-transitive graphs than previously thought. In fact, the researchers discovered new graph types that had not been seen before, shedding light on the diversity of these structures. This discovery has significant implications for computer science, as it opens up new avenues for the design and analysis of algorithms.
Another important aspect of Conder and Potočnik’s work is their development of a new method for lifting a prescribed group of automorphisms from a smaller graph to a larger one. This technique allows researchers to construct new graphs with specific properties, which can be used in various applications, such as coding theory and cryptography.
The completion of this catalog marks a significant milestone in the study of cubic edge-transitive graphs. It provides a solid foundation for future research and has far-reaching implications for various fields. Conder and Potočnik’s work demonstrates the power of collaboration between mathematicians and computer scientists, highlighting the importance of interdisciplinary approaches to solving complex problems.
Cite this article: “Unlocking the Secrets of Cubic Edge-Transitive Graphs”, The Science Archive, 2025.
Mathematics, Graph Theory, Cubic Edge-Transitive Graphs, Automorphism Group, Computer Science, Coding Theory, Cryptography, Algorithms, Geometry, Combinatorics
Reference: Marston Conder, Primož Potočnik, “Edge-transitive cubic graphs: Cataloguing and Enumeration” (2025).