Wednesday 09 April 2025
A team of researchers has made a significant breakthrough in understanding how complex networks function and behave. By studying the properties of supermodular functions, they’ve been able to develop new algorithms for solving problems that were previously thought to be intractable.
Supermodular functions are a type of mathematical object that can be used to model complex systems, such as social networks or transportation networks. They have certain properties that make them useful for understanding how these systems behave and respond to changes.
One of the key challenges in studying supermodular functions is developing efficient algorithms for solving problems involving these functions. These algorithms need to be able to take into account the complex interactions between different components of the system, while also being fast enough to be practical.
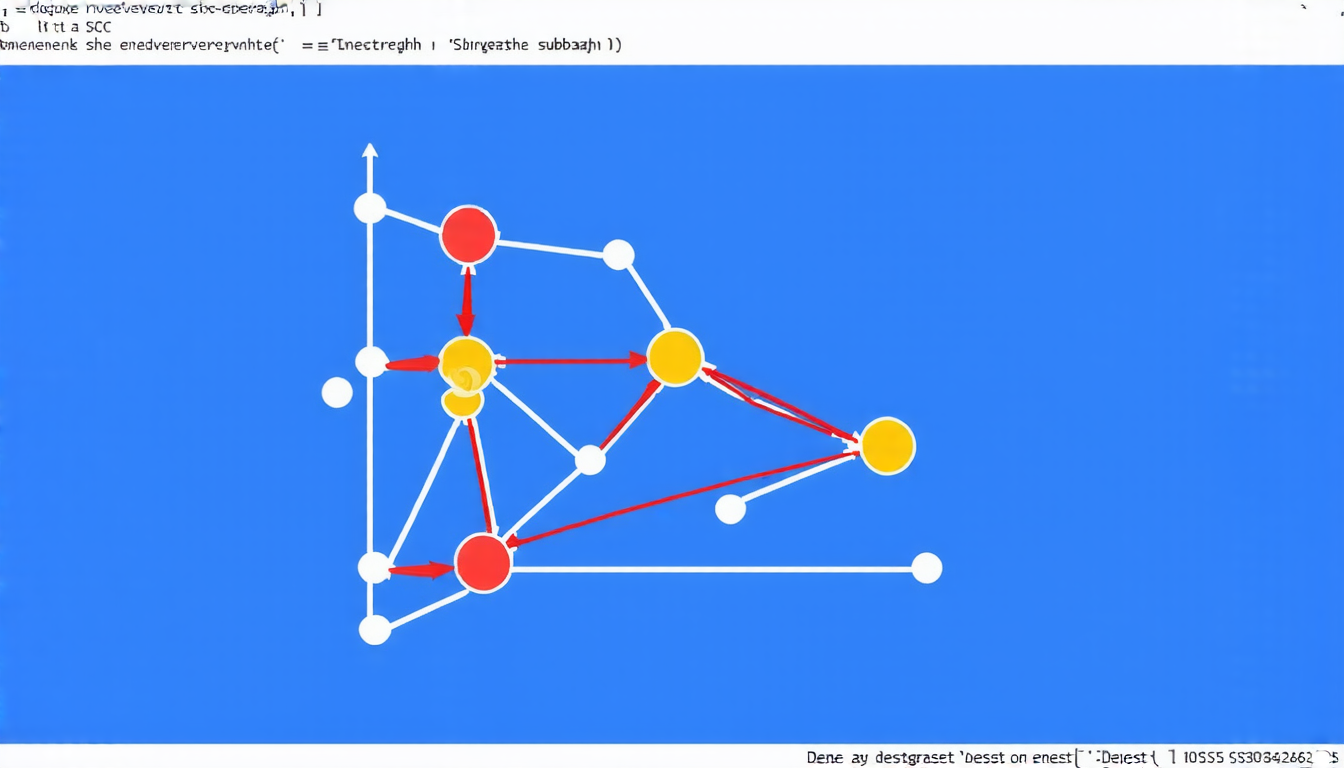
The researchers’ new algorithm is designed to solve a specific problem called the densest subgraph problem. This problem involves finding the subset of vertices in a graph that has the highest density, or number of edges per vertex. The algorithm uses a combination of mathematical techniques and clever data structures to efficiently search for the optimal solution.
One of the key innovations of the algorithm is its ability to adapt to changing conditions. In many real-world systems, the properties of the system can change over time, such as the addition or removal of vertices in a network. The researchers’ algorithm is able to quickly adjust to these changes and continue searching for the optimal solution.
The potential applications of this new algorithm are vast. It could be used to optimize the performance of complex systems, such as transportation networks or communication networks. It could also be used to identify patterns and relationships in large datasets, such as social media or financial transactions.
In addition to its practical applications, the researchers’ work has also shed light on some fundamental questions about supermodular functions. For example, they’ve shown that certain types of supermodular functions are more difficult to optimize than others, which could have important implications for our understanding of complex systems.
Overall, this new algorithm represents a major advance in the field of network science and has the potential to revolutionize the way we understand and interact with complex systems.
Cite this article: “Unlocking Densest Subgraphs: A Journey Through Graph Theory and Matroid Theory”, The Science Archive, 2025.
Supermodular Functions, Network Science, Algorithms, Complex Networks, Graph Theory, Optimization, Densest Subgraph Problem, Data Structures, Machine Learning, Computer Science