Friday 21 March 2025
Graph theory has long been a fascinating field of study, with mathematicians and computer scientists working to understand the properties and behaviors of complex networks. One area that has garnered significant attention in recent years is the study of cycles within graphs – specifically, the number of chords that can exist within these cycles.
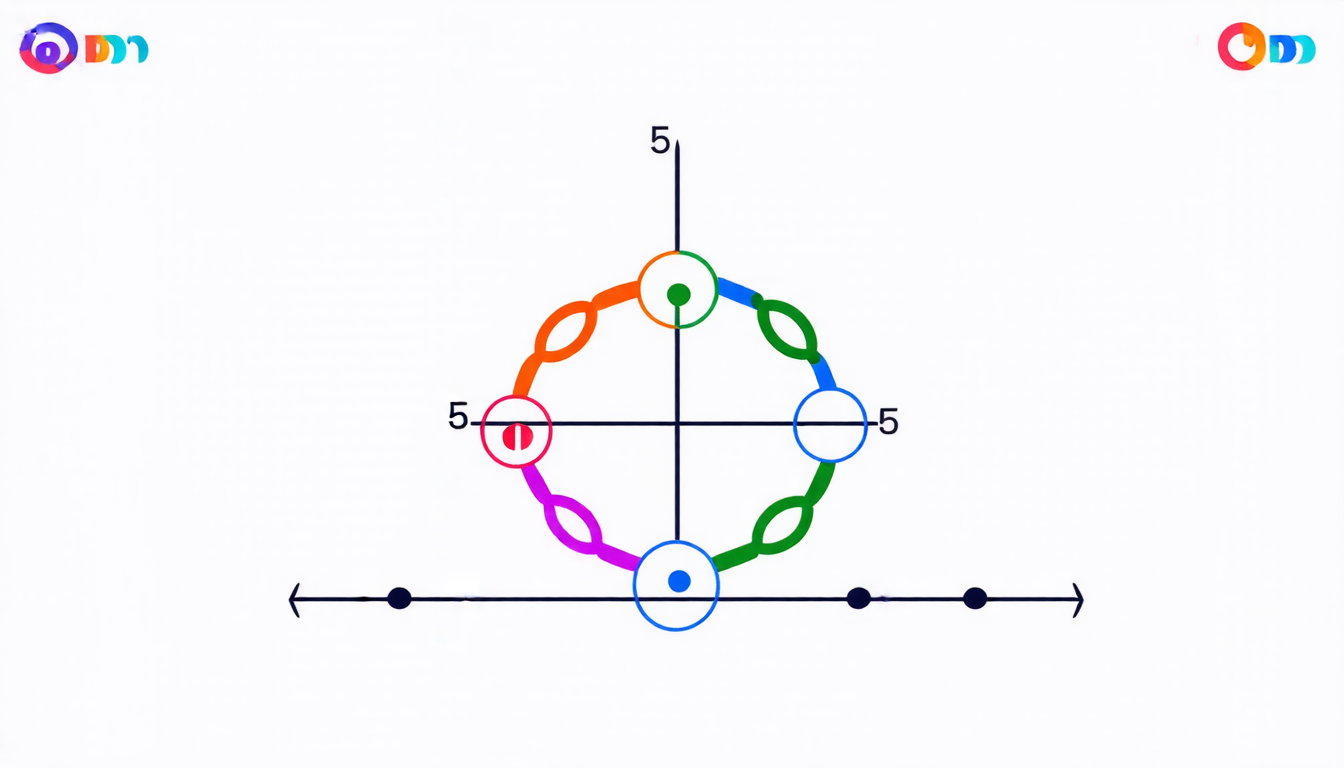
A chord is essentially an edge that connects two non-consecutive vertices on a cycle. The more chords a cycle contains, the more complex its structure becomes. Researchers have long been interested in understanding the relationship between the minimum degree of a graph and the number of chords it can contain.
Recently, a team of mathematicians made a significant breakthrough in this area by proving that every graph with a minimum degree of at least k has a cycle containing at least (k+1)(k-2)/2 chords. This result is remarkable not only because it provides a new insight into the structure of graphs but also because it has important implications for computer science and network analysis.
To put this discovery into perspective, consider a graph with a minimum degree of 3 – in other words, every vertex is connected to at least three other vertices. According to the team’s result, such a graph must contain a cycle with at least five chords. This may seem like a relatively simple observation, but it has significant consequences for our understanding of complex networks.
One area where this discovery could have a major impact is in the design of efficient algorithms for network analysis. By understanding the structure of cycles within a graph, researchers can develop more effective methods for identifying patterns and anomalies within large datasets.
Another potential application of this result lies in the field of computer science, where it could be used to improve the efficiency of data structures such as graphs and networks. By optimizing the number of chords within these structures, developers may be able to create faster and more reliable algorithms for tasks such as network routing and scheduling.
The implications of this discovery extend far beyond the realm of pure mathematics, however. The study of cycles and chords has important consequences for our understanding of complex systems in biology, physics, and other fields. By analyzing the structure of these networks, researchers may be able to gain new insights into the behavior of complex systems and develop more effective strategies for modeling and predicting their behavior.
Overall, this breakthrough is an exciting development that promises to have significant implications for a wide range of fields.
Cite this article: “Unlocking the Secrets of Graph Cycles: A Breakthrough in Network Analysis”, The Science Archive, 2025.
Graph Theory, Cycles, Chords, Minimum Degree, Network Analysis, Computer Science, Data Structures, Algorithms, Complex Systems, Mathematics.